Customers are often concerned with what flowrates are compatible with our Multipurpose flow cells and sample systems. To help answer this question Guided Wave has developed a Reynolds Number calculator, which is located towards the bottom of this webpage. The same concerns can also be applied to our family of insertion transmission spectroscopy probes, but we will limit our discussion to the less complex geometry of the flowcell.

The Relationship Between Analyzer Noise and Reynolds Number

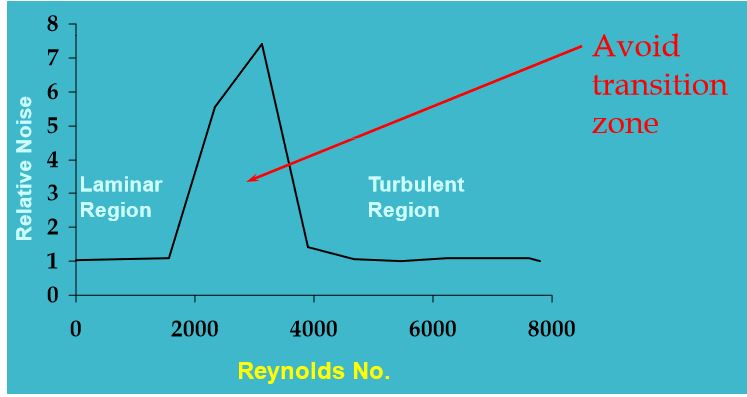
The question of flow rate cannot be answered without more information regarding the sample. To achieve stable Near Infrared Spectroscopy readings, a steady flow of fluid must be passing through the optical beam during the measurement. The flow can either be smooth and laminar or turbulent. Flowrate alone cannot be determined without understanding the fluid dynamics such as the kinematic viscosity and the diameter of the pipe passing through the flowcell. Additionally, if the flow has particulates, bubbles, or mixed phases which will vary the chemical composition and index of refraction during the measurement period, then the NIR measurement will not be stable.

What is Viscosity?

The textbook definition of viscosity is the resistance of the fluid to flow or deform. Said another way, viscosity is the thickness of the fluid. The classic example is molasses which is thicker and thus has a higher viscosity than water. This may be referred to as the absolute or dynamic viscosity of the liquid.

What is Kinematic Viscosity?

The kinematic viscosity of a fluid is the ratio of the viscosity of the fluid to the fluid’s density. For most fuel and other liquids, fluid dynamic values have already been tabulated. For example, 100% ethanol at 25C has the following known properties.

What is a Reynolds Number?

The Reynold Number (Re) is a mathematical equation helps to determine if the flow in the pipe is Laminar Flow or Turbulent Flow. This is achieved by relating the kinematic viscosity of the fluid, diameter of the pipe, and the linear speed or flowrate of the liquid sample. See equation 1

*To achieve laminar flow Re < 2100 or turbulent flow Re> 3000

Relating the Flow Rate to the Fluid Velocity.

To calculate the linear velocity of the fluid we use equation 2, shown below. Our 10 mm pathlength Multipurpose Flowcell has an approximate internal surface area of 9.37×10^-5 m².

Calculating the Reynolds Number for Ethanol.

If we assume the flow rate through the inner 0.43-inch pipe diameter (1/2 inch OD pipe) is 3.0 L/min, then we get:

Fluid Velocity = (4*3(L/min)) / (3.14*(0.010922m)) = 0.53 meters per second

Now applying this value into equation 1 with the tabulated value for viscosity we see that:

Re= 0.53 m/s * 0.010922m / 0.000001 m²/s ≈ 4500

Because a Re of 4500 is greater than 3000, we can be confident that the flow through the optical beam of the flowcell is turbulent. Thus measurement of the sample liquid should result in high-quality spectra. This again assumes that the liquid sample passing through the flowcell is heterogeneous and free of particulate matter or other contaminants.

Interested in determining what your Renolds number is? Check out the Reynolds number calculator below.

The U.S. Department of Energy announced that a research and development project submitted by Guided Wave Inc. has been selected as an award winner in its Industrial Energy Efficiency Grand Challenge. This initiative provides funding to various research and development projects across the country for the development of transformational industrial processes and technologies that can significantly reduce greenhouse gas emissions throughout the industrial sector.

As a grantee, Guided Wave, a leading manufacturer of process chemical analyzers, will receive significant funding towards the development of an advanced on-line sensor for polymer processing. “This is a unique technique to control the plasticizing process,” states, Guided Wave, Corporate Fellow Dr. Terry Todd. “A high rate of scrap recycle is caused due to color problems. This new sensor may reduce this scrap significantly, thus minimizing energy consumption in the polymer extrusion process.”

According to the Department of Energy, American industry accounts for more than 30 percent of the energy used nationwide, is responsible for 27 percent of the country’s carbon emissions, and supports nearly 13 million core manufacturing jobs.  With such a large impact on the nation’s economic and environmental interests, the industrial sector remains a major part of the Nation’s clean energy equation. This funding will promote breakthrough achievements in the development of energy-efficient technologies and practices that will lower the energy demand of industry, open up new potential markets, and enhance the competitiveness of American business.